Back to Main Menu

Gauss' Law

Gauss's Law allows us to calculate the electric flux density (D) associated with a symmetrical distribution of charges. From this, the electric field intensity (E) can also be derived.

Gauss's Law states that the total outward electric flux over any closed surface is equal to the free charge enclosed by that surface. In symbolic form:

      /
     |  -     -
    (|) D ·ds = Q
     |
     /s

This is a very useful relation, because if we have a convenient Gaussian surface (a symmetrical one over which the normal component of D is constant), we can use this relation to compute the D field and the E field everywhere, without resorting to Coulomb's law.

Why must symmetry be present? Consider the charge distributions below and the surfaces associated with them. The first surface is a sphere and the second is a mangled globe. Each contains a charge of Q.

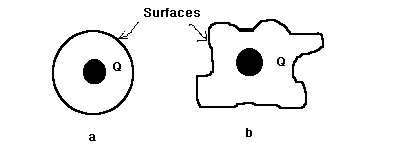
It would be fairly easy to compute the fields associated with the charge distributions shown. However, let's see what insight this gives us into Gauss's Law.

Gauss's law tells us that the total outward flux (or flow) of the D field (and thus the E field) depends only on the enclosed free charge. So which of the following is true :

☞ The total outward flux of surface (a) is greater.
☞ The total outward flux of surface (b) is greater.
☞ The total outward flux in (a) and (b) are equal.

Now let's look at how the symmetry involved can help us to calculate the fields. Since the normal component of the D field in part (b) is not constant over the entire surface, relating this flux to the enclosed charge is going to be nearly impossible. However, since the normal component is constant in (a), and spherical surface is easy to represent mathematically, we can solve for D as follows(in spherical coordinates) :

     /           /2π    /2π
    |  -   -    |       |     2                  ^
  (|) D·ds = |      | D  r sinΘ dΘ dø r = Q
    |            |      |  r
    /s          /       /

Therefore,

     2
4πr  D = Q
         r

_         Q     ^
D = ------- r
              2
         4πr

        _
_      D
E = ---
       ε
          0

This gives the exact same result as Coulomb's Law in a very simple form. Remember, cases of high geometrical symmetry are often easiest to solve for using Gauss's Law.

Back to Main Menu